Kleinplaneten-Tagung
2025

Könnte man von der Erde aus Kleinplanetenmonde mit Amateumitteln direkt nachweisen?
Was sagt die Theorie?
Theoretisch wird der mögliche Abstand eines Kleinplanetenmondes
durch die Hill-Sphäre definiert.
Sie entspricht etwa dem Abstand zu den Lagrange-Punkten 1 oder 2.
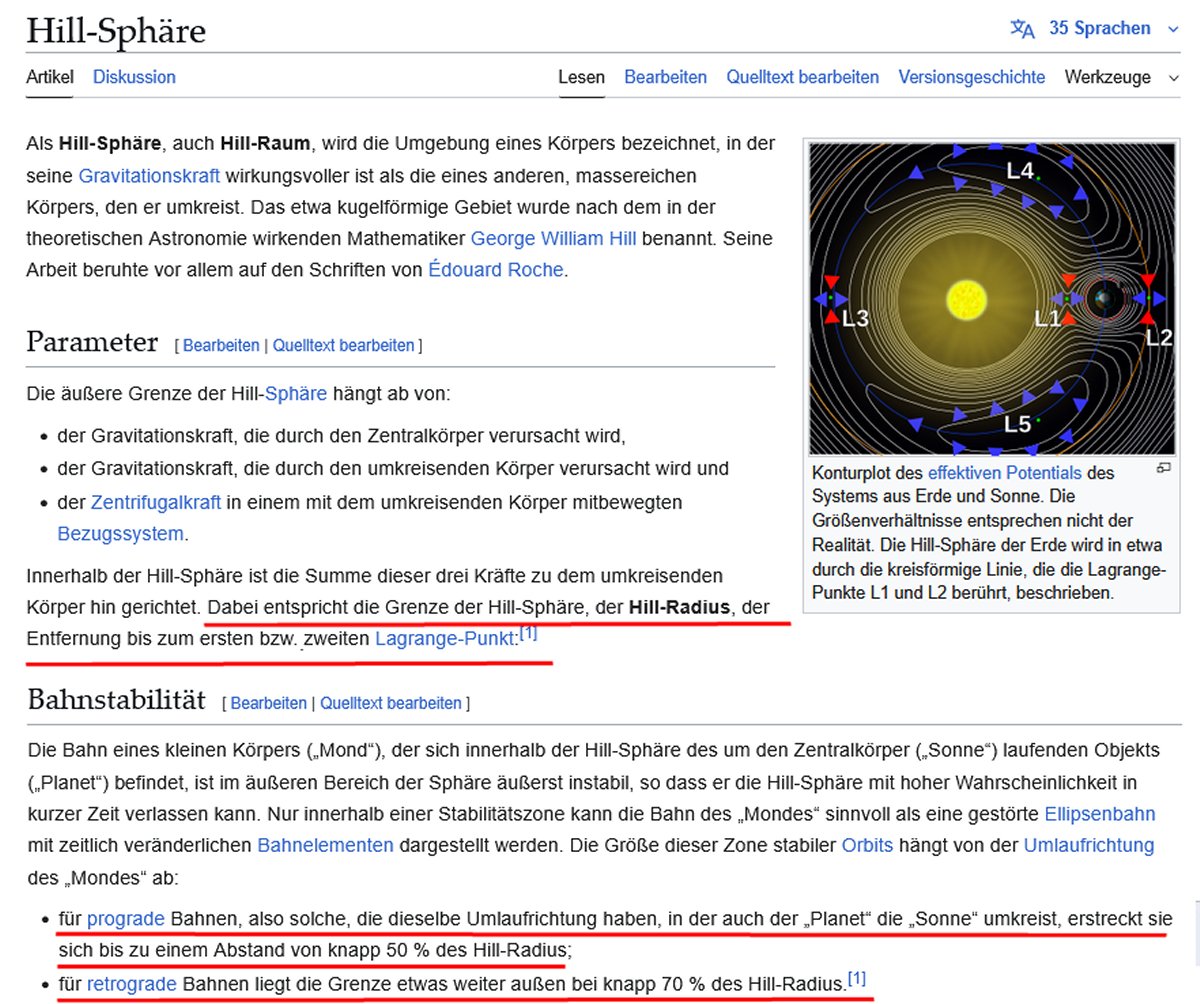
Stabil für prograde Bahnen sind etwa 50% der
Hillsphäre.
Für retrograde Bahnen 70%. Darum sind die
äußeren
Satelliten des Jupiters oft retrograd.
Die Hillsphäre lässt sich angenehm leicht rechnen.
Hier ein
Beispiel für einen 100 km Asteroiden:

Leider sind im Hauptgürtel durch Störungen des
Jupiters in der Praxis die
Hill-Sphären so klein, dass man sie mit Amateurmitteln nicht
auflösen kann.
Die einzige bekannte Ausnahme jenseits des Hauptgürtels ist
Charon der Mond von Pluto:
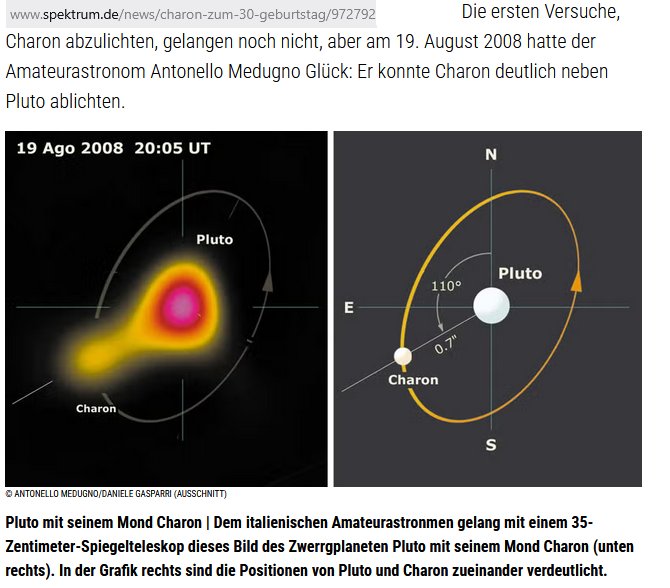
Die
Alternative zum Nachweis der Monde ist die Photometrie. Es werden
jedoch
große Monde benötigt:

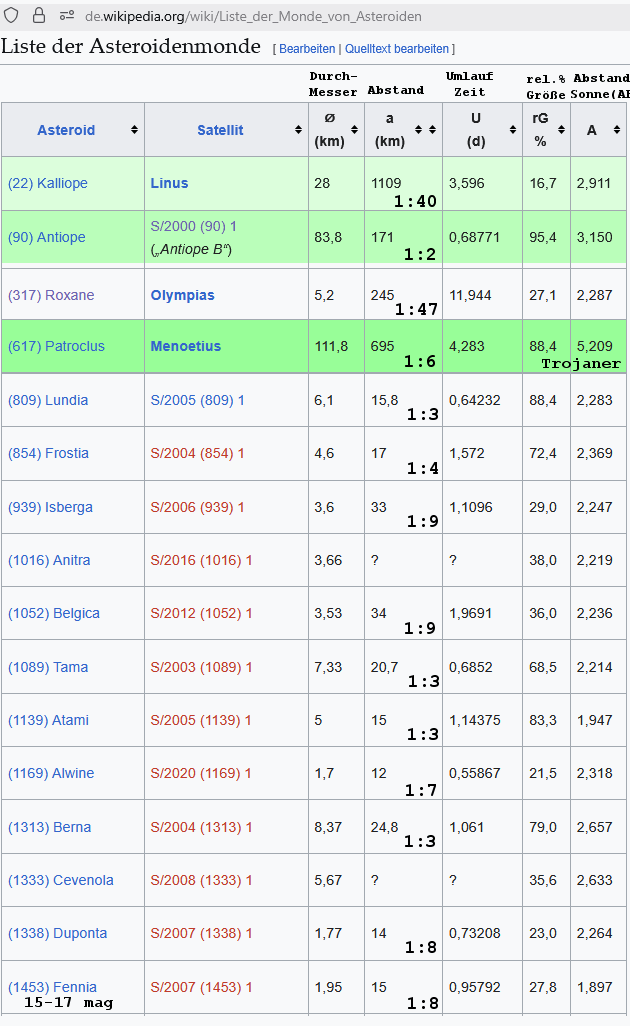
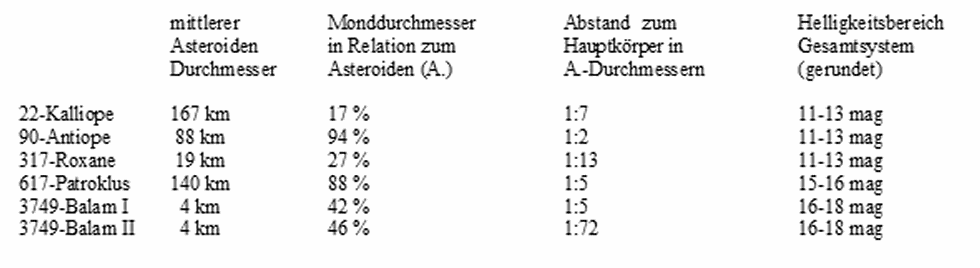
In der Liste der Satellitenmonde bei Wikipedia finden sich einige
interessante Kandidaten:
Doch leider gibt es kaum Ephemeriden. Es gibt in der Literatur
Entdeckungsmeldungen ...und das wars.
Die meisten Teams existieren nicht lang genug um die Umlaufzeit von
>4 Jahren abzudecken.
Zudem liefern 4 Varianten von Ereignissen die gleiche Amplitude:
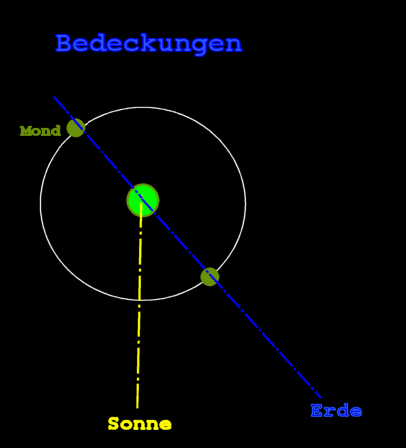
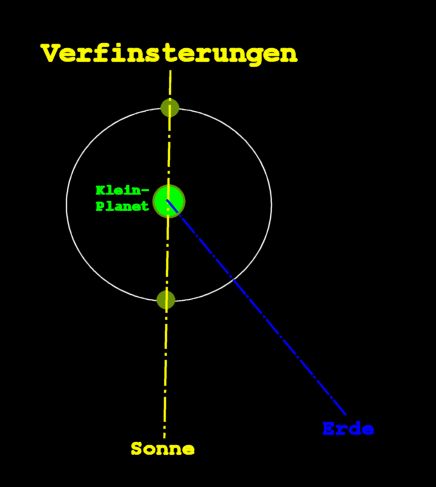
Die einzige (gefundene) Stelle mit wenigen Ephemeriden gibt es beim
Sternberg-Institut:

Die Schnittmenge ist:
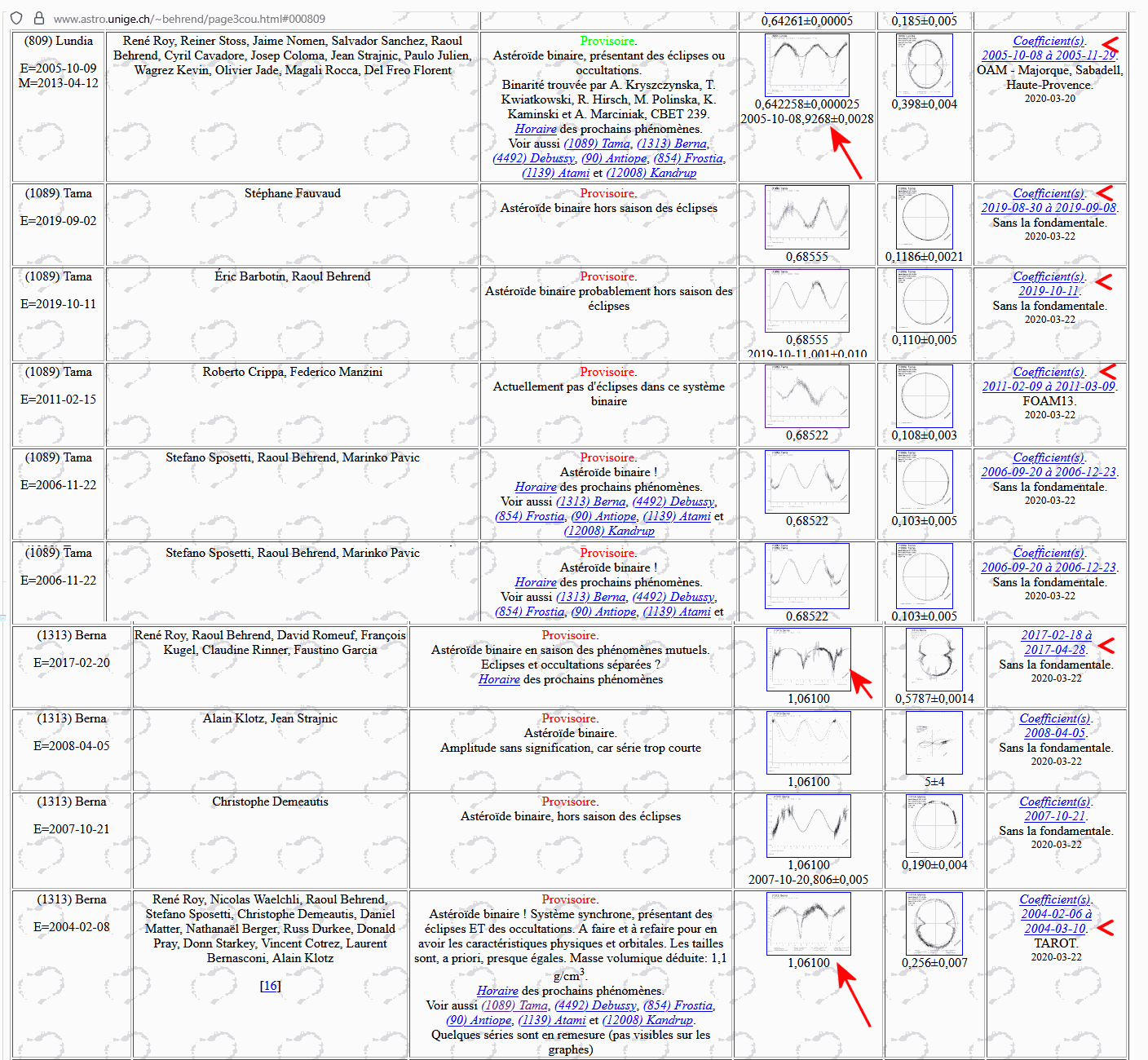
Beobachtungstipps gibt es auf der Seite von Roul Behrend über
die
Messkurven vergangener Bedeckungen und Verfinsterungen.
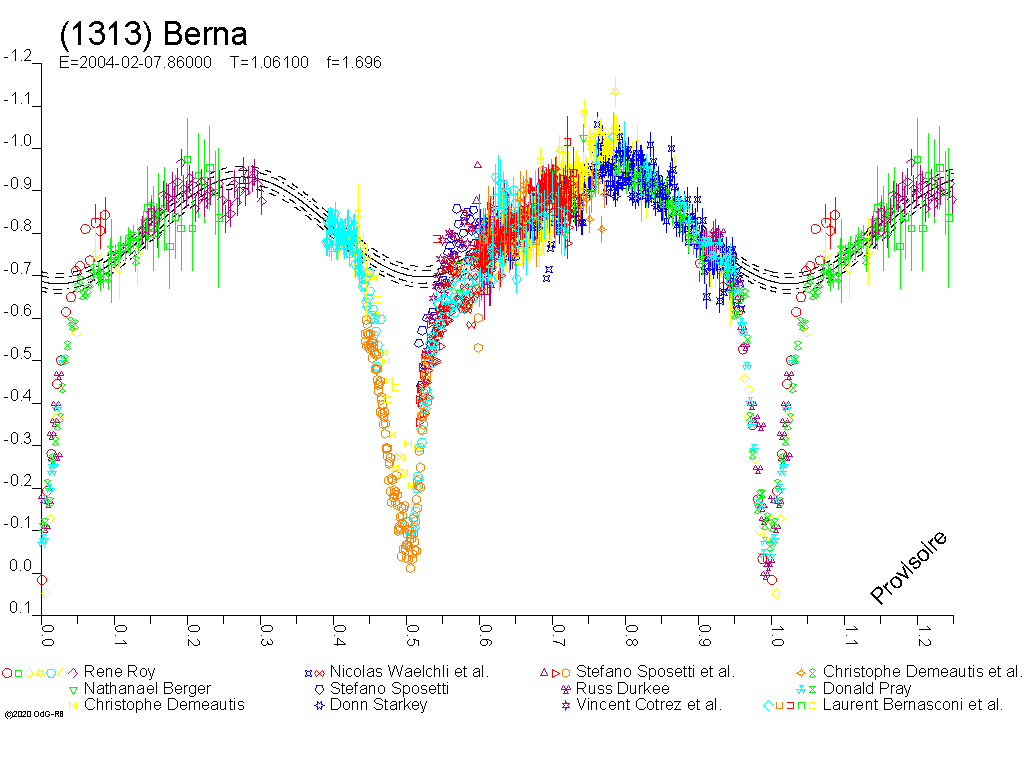
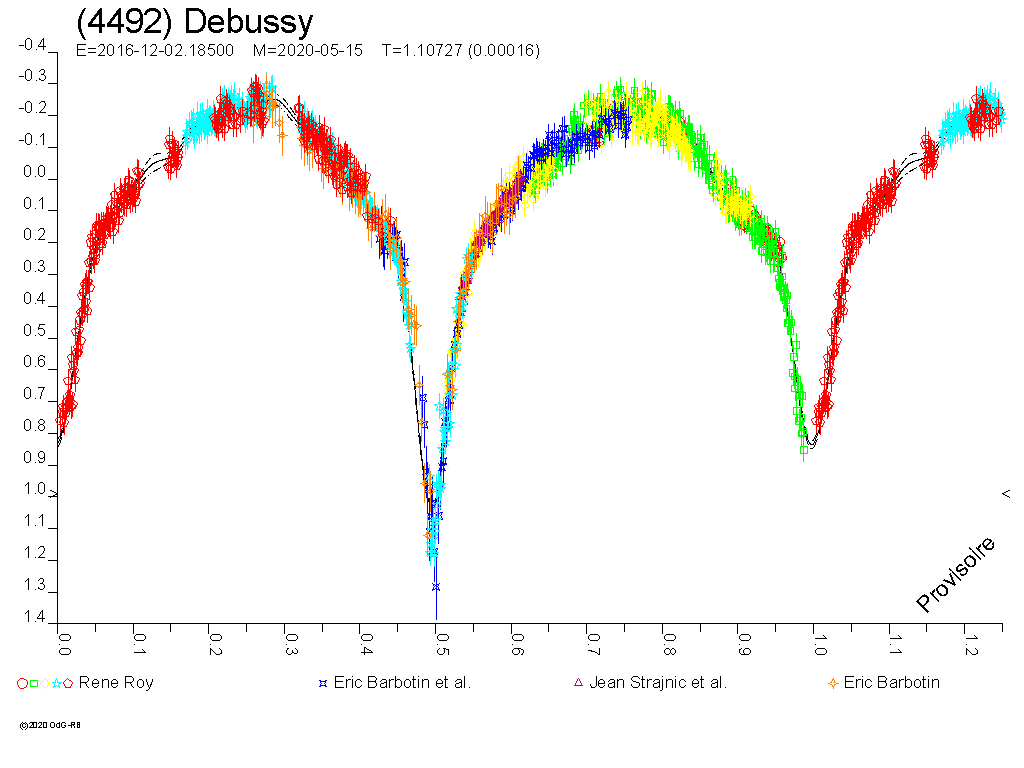
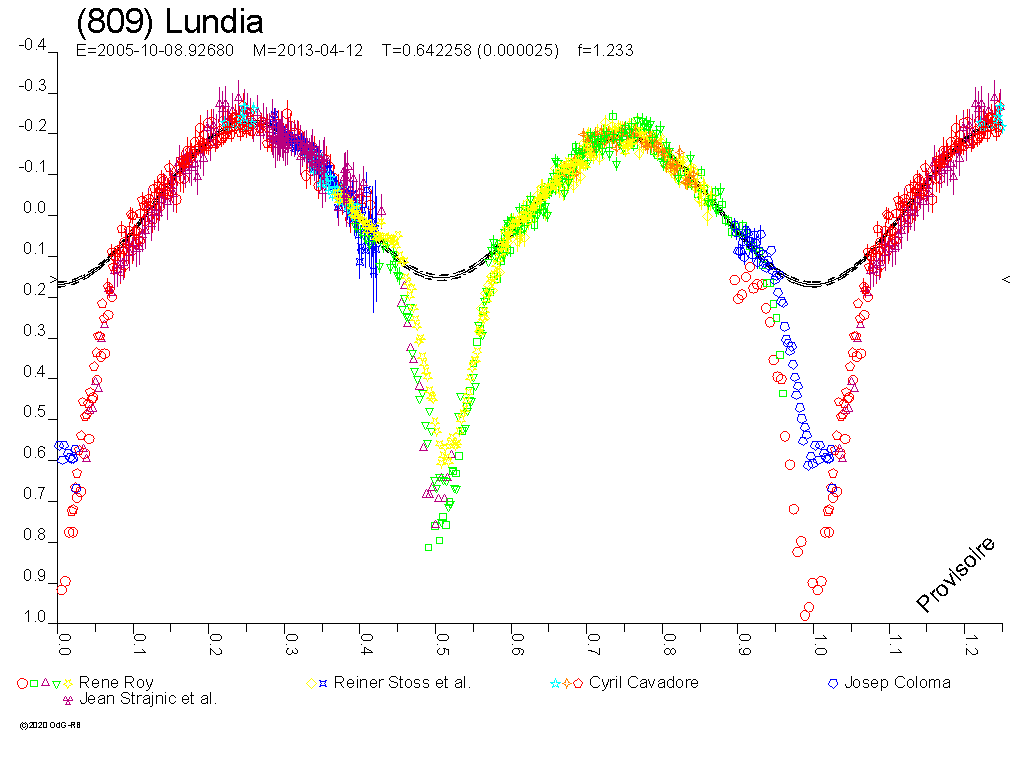
Woran erkennt man überhaupt die Lichtkurve eine
Kleinplaneten-Mondes? Ein Mond kann existieren ohne das man ihn sieht.
Der Mess-Zeitpunkt muss Bahnneigung um die Sonne und zur Bahnneigung im
Mondsystem passen.
.....Schauen wir auf ein Propeller sehen wir nichts.....
Die Lage des Systems kann man mit einer Sternbedeckung prüfen.
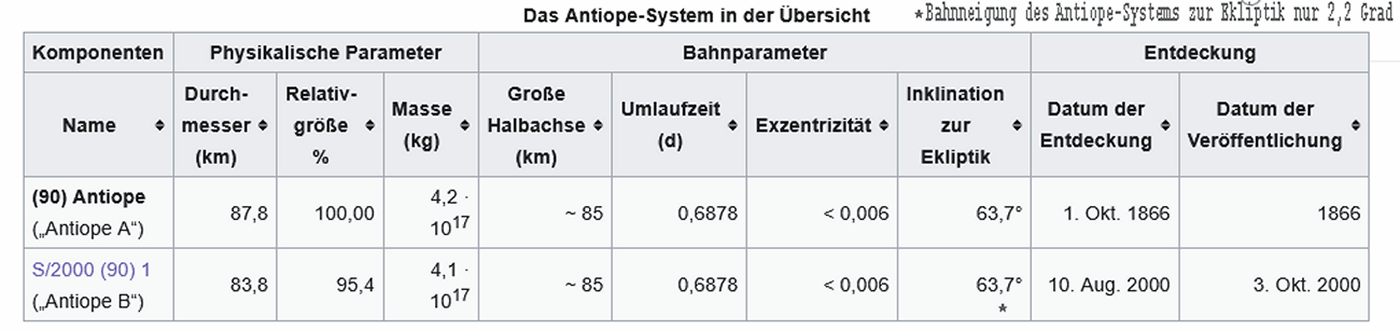
Gut erforscht ist 90-Antiope:

Passt der Zeitpunkt zur Bahnneigung kann man im Differenzverfahren bei
der Photometrie den Mond rausarbeiten:
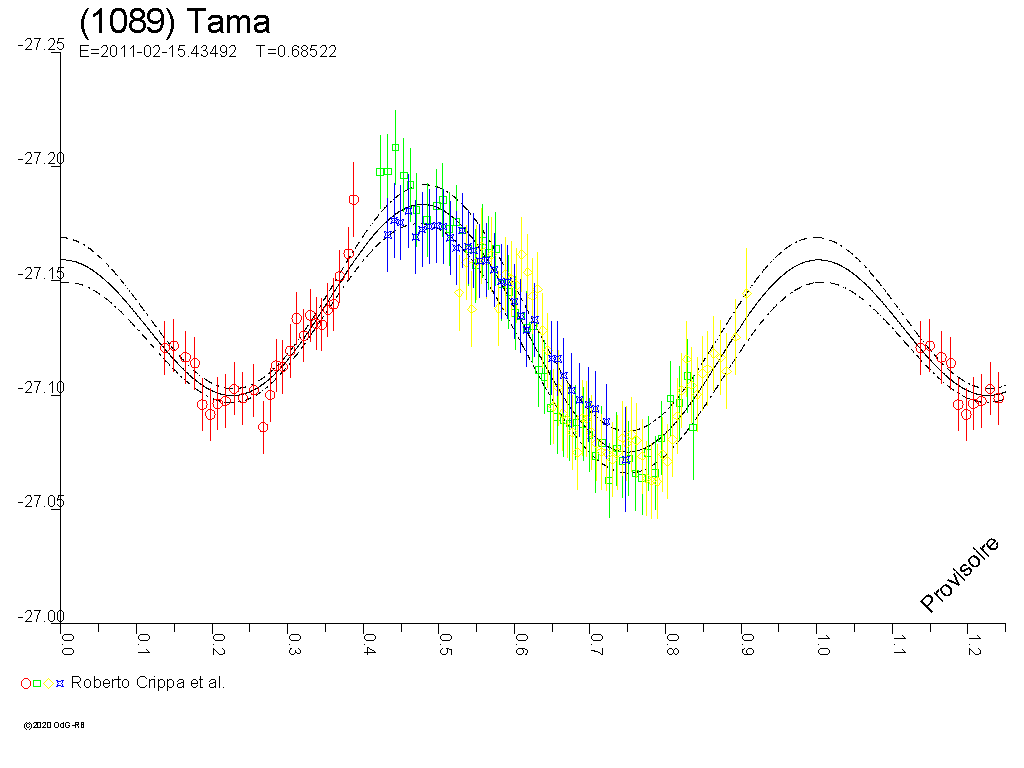
Bei einigen Systemen gibt es charakteristische V-förmige
Einschnitte. Die sind gut sichtbar wenn der Hauptkörper rund
ist: